Lớp 12 - SBT Toán học Giải bài 1.10, 1.11, 1.12, 1.13 trang 20 Sách bài tập Hình học 12
Bài 1.10 trang 20 sách bài tập (SBT) – Hình học 12
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 600. Hãy tính thể tích của khối chóp đó.
Hướng dẫn làm bài:
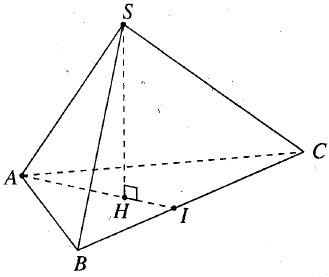
Kẻ \(SH \bot (ABC)\) . Đường thẳng AH cắt BC tại I.
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của \(\Delta ABC\) .
Do đó \(AI = {{\sqrt 3 } \over 2}a,AH = {2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a,\widehat {SAH} = {60^0}\)
\(SH = AH.\tan {60^0} = {{\sqrt 3 } \over 3}a.\sqrt 3 = a\)
Thể tích khối chóp S.ABC là: \(V = {1 \over 3}.{1 \over 2}.{{\sqrt 3 } \over 2}a.a.a = {{\sqrt 3 } \over {12}}{a^3}\)
Bài 1.11 trang 20 sách bài tập (SBT) – Hình học 12
Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 600.Hãy tính thể tích của khối chóp đó.
Hướng dẫn làm bài:
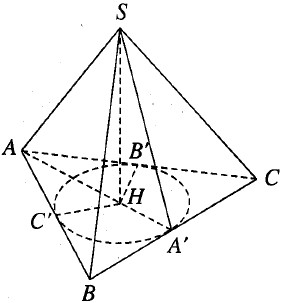
Kẻ \(SH \bot (ABC)\) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có \(SA' \bot BC,SB' \bot CA,SC' \bot AB\)
Từ đó suy ra \(\widehat {SA'H} = \widehat {SB'H} = \widehat {SC'H} = {60^0}\).
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó, AA’2 = AB2 – BA’2 = 25a2 – 9a2 = 16a2
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó \({S_{ABC}} = {1 \over 2}6a.4a = 12{a^2} = pr = 8ar\)
Từ đó suy ra \(r = {3 \over 2}a\)
Do đó \(SH = HA'.\tan {60^0} = {{3a} \over 2}\sqrt 3 = {{3\sqrt 3 } \over 2}a\)
Thể tích khối chóp là \(V = {1 \over 3}.12{a^2}.{{3\sqrt 3 } \over 2}a = 6\sqrt 3 {a^3}\).
Bài 1.12 trang 20 sách bài tập (SBT) – Hình học 12
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c.
a) Hãy tính thể tích khối chóp S.ADE
b) Tính khoảng cách từ E đến mặt phẳng (SAB).
Hướng dẫn làm bài:
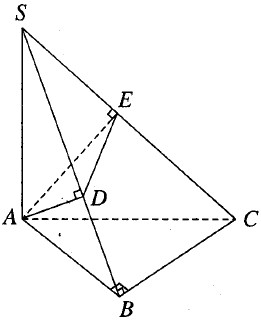
a) Ta có \(\left\{ {\matrix{{BC \bot SA} \cr {BC \bot AB} \cr} } \right. \Rightarrow BC \bot (SAB)\)
Vì \(AD \subset (SAB)\) nên \(AD \bot BC\)
Mặt khác \(AD \bot SB\) nên \(AD \bot (SBC)\)
Từ đó suy ra \(AD \bot SC\)
\(\left\{ {\matrix{{SC \bot AE} \cr {SC \bot AD} \cr} } \right. \Rightarrow SC \bot (ADE) \Rightarrow SC \bot DE\) hay \(SE \bot (ADE)\) .
Trong tam giác vuông SAB ta có: \(SA.AB = AD.SB \Rightarrow AD = {{AB.SA} \over {SB}} = {{ac} \over {\sqrt {{a^2} + {c^2}} }}\)
Tương tự, trong tam giác vuông SAC ta có: \(AE = {{SA.AC} \over {SC}} = {{c\sqrt {{a^2} + {b^2}} } \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Do \(AD \bot (SBC)\) nên \(AD \bot DE\) . Từ đó suy ra:
\(DE = \sqrt {A{E^2} - A{D^2}}\)
\( = \sqrt {{{{c^2}({a^2} + {b^2})} \over {{a^2} + {b^2} + {c^2}}} - {{{a^2}{c^2}} \over {{a^2} + {c^2}}}}\)
\( = {{{c^2}b} \over {\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}\)
\(SE = \sqrt {S{A^2} - A{E^2}}\)
\( = \sqrt {{c^2} - {{{c^2}({a^2} + {b^2})} \over {{a^2} + {b^2} + {c^2}}}}\)
\( = {{{c^2}} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Vậy \({V_{S.ADE}} = {1 \over 3}.{1 \over 2}AD.DE.SE \)
\(= {1 \over 6}{{ac} \over {\sqrt {{a^2} + {c^2}} }}.{{{c^2}b} \over {\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}.{{{c^2}} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( = {{ab{c^5}} \over {6({a^2} + {b^2} + {c^2})({a^2} + {c^2})}}\)
b) Gọi d là khoảng cách từ E đến mặt phẳng (SAB)
Ta có: \(SD = \sqrt {S{A^2} - A{D^2}} = \sqrt {{c^2} - {{{a^2}{c^2}} \over {{a^2} + {c^2}}}} = {{{c^2}} \over {\sqrt {{a^2} + {c^2}} }}\)
\({V_{S.ADE}} = {V_{E.SAD}} = {1 \over 3}.{1 \over 2}SD.AD.d \)
\(= {1 \over 6}{{{c^2}} \over {\sqrt {{a^2} + {c^2}} }}{{ac} \over {\sqrt {{a^2} + {c^2}} }}d \)
\(= {1 \over 6}{{a{c^3}} \over {{a^2} + {c^2}}}d\)
Kết hợp với kết quả trong câu a) ta suy ra \(d = {{b{c^2}} \over {{a^2} + {b^2} + {c^2}}}\)
Bài 1.13 trang 20 sách bài tập (SBT) – Hình học 12
Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.
Hướng dẫn làm bài:
Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, hA , hB , hC , hD lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).
Khi đó ta có:
\(V = {V_{MBCD}} + {V_{MCDA}} + {V_{MDAB}} + {V_{MABC}}\)
\(= {1 \over 3}S({h_A} + {h_B} + {h_C} + {h_D})\)
Từ đó suy ra \({h_A} + {h_B} + {h_C} + {h_D} = {{3V} \over S}\)
congdong.edu.vn