Bài 5.7 trang 14 Sách bài tập (SBT) Vật Lí 12
Hai dao động điều hoà cùng phương, cùng chu kì có phương trình lần lượt là : \({x_1} = 4\cos \left( {10\pi t + {\pi \over 3}} \right)\left( {cm} \right)\,;{x_2} = 4\cos \left( {10\pi t + \pi } \right)\left( {cm} \right)\). Tìm phương trình của dao động tổng hợp.
Hướng dẫn giải chi tiết
Xem hình 5.4G
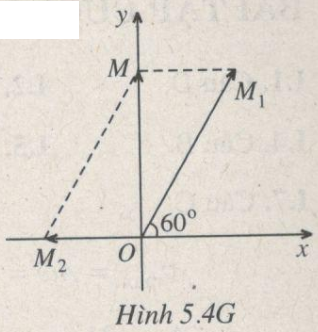
Từ giản đồ Fre-nen ta thấy vecto \(\overrightarrow {OM} \) nằm trên trục Oy
Suy ra :
\(\eqalign{
& OM = 2\sqrt 3 cm;\,\varphi = {\pi \over 2} \cr
& x = 2\sqrt 3 cos\left( {10\pi t + {\pi \over 2}} \right)cm \cr} \)
Bài 5.8 trang 14 Sách bài tập (SBT) Vật Lí 12
Hai dao động điều hoà cùng phương, cùng chu kì có phương trình lần lượt \({x_1} = 6\sin {{5\pi t} \over 2}\left( {cm} \right)\,;{x_2} = 6\cos {{5\pi t} \over 2}\left( {cm} \right)\)Tim phương trình của dao động tổng hợp.
Hướng dẫn giải chi tiết
Xem hình 5.5 G
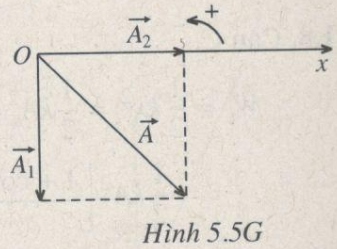
\(\eqalign{
& {x_1} = 6\sin {{5\pi t} \over 2}\left( {cm} \right)\, = 6\cos \left( {{{5\pi t} \over 2} - {\pi \over 2}} \right)cm \cr
& {x_2} = 6\cos {{5\pi t} \over 2}\left( {cm} \right) \cr
& A = {A_1}\sqrt 2 = 8,485 \approx 8,5\,cm;\,\varphi = - {\pi \over 4} \cr
& x = 8,5cos\left( {{{5\pi } \over 2}t - {\pi \over 4}} \right)cm \cr} \)
Bài 5.9 trang 15 Sách bài tập (SBT) Vật Lí 12
Hai dao động điều hoà cùng phương, cùng tần số, có phương trình lần lượt là : \({x_1} = 6\cos \left( {\omega t - {\pi \over 4}} \right)\left( {cm} \right)\, = 6\cos \left( {\omega t - {{5\pi } \over {12}}} \right)cm\). Tìm phương trình của dao động tổng hợp.
Hướng dẫn giải chi tiết
Xem giản đồ Fre-nen (H.5.6G)
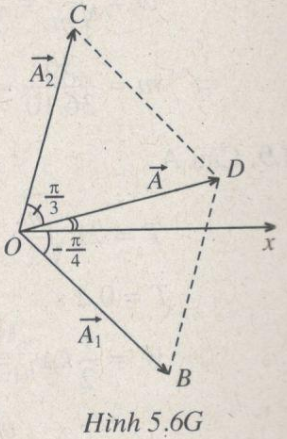
\(\left| {\overrightarrow {{A_1}} } \right| + \left| {\overrightarrow {{A_2}} } \right| = 6\,cm \Rightarrow \Delta COD\,\) cân
\(\eqalign{
& \widehat {COB} = {\varphi _2} + \left| {{\varphi _1}} \right| = {{5\pi } \over {12}} + {\pi \over 4} = {{2\pi } \over 3} \cr
&\Rightarrow \widehat {COD} = {\pi \over 3} \cr} \)
Pha ban đầu của dao động tổng hợp là :
\(\eqalign{
& \varphi = {\varphi _2} - {\pi \over 3} = {{5\pi } \over {12}} - {\pi \over 3} = {\pi \over {12}} \cr
& \left| {\overrightarrow A } \right| = \left| {\overrightarrow {{A_1}} } \right| = \left| {\overrightarrow {{A_2}} } \right| \cr} \)