Bài 5 trang 98 sgk hình học 11
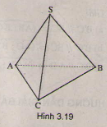
Cho hình chóp tam giác \(S.ABC\) có \(SA = SB = SC\) và có \(\widehat{ABC}= \widehat{BSC}=\widehat{CSA}.\) Chứng minh rằng \(SA ⊥ BC, SB ⊥ AC, SC ⊥ AB\).
Giải
(h.3.19)
\(\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB})\)
\(=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\)
\(= SA.SC.\cos\widehat{ASC} - SA.SB.\cos\widehat{ASB} = 0\).
Vậy \(SA ⊥ BC\).
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\)
\(=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(= SB.SC.\cos\widehat{BSC} - SB.SA.\cos\widehat{ASB} = 0\).
Vậy \(SB ⊥ AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\)
\(=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(= SC.SB.\cos\widehat{BSC} - SC.SA.\cos\widehat{ASC} = 0\).
Vậy \(SC ⊥ AB\).
Bài 6 trang 98 sgk Hình học 11
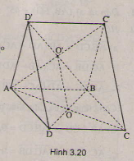
Trong không gian cho hai hình vuông \(ABCD\) và \(ABC'D'\) có chung cạnh \(AB\) và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm \(O\) và \(O'\). Chứng minh rằng \(AB ⊥ OO'\) và tứ giác \(CDD'C'\) là hình chữ nhật.
Giải
(h.3.20)
\(\overrightarrow{AB}.\overrightarrow{OO'}=\overrightarrow{AB}.(\overrightarrow{AO'}-\overrightarrow{AO})\)
\(=\overrightarrow{AB}.\overrightarrow{AO'}-\overrightarrow{AB}.\overrightarrow{AO}\)
\(= AB.AO'.\cos45^{0} - AB.AO.\cos45^{0}\)
\(= 0\).
Vậy \(AB ⊥ OO'\).
Mặt khác ta có \(CD\) song song và bằng \(C'D'\) nên \(CDC'D'\) là hình bình hành. \(AB\) vuông góc với \(BC\) và \(BC'\) nên \(AB\) vuông góc với \((BCC')\)\( \Rightarrow AB ⊥ CC'\); mà \(CD // AB \Rightarrow CD ⊥ CC' \Rightarrow CDD'C'\) là hình chữ nhật.
Bài 7 trang 98 sgk Hình học 11
Cho \(S\) là diện tích tam giác \(ABC\). Chứng minh rằng:
\(S=\frac{1}{2}\sqrt{\overrightarrow{AB}^{2}.\overrightarrow{AC}^{2}-(\overrightarrow{AB}.\overrightarrow{AC})^{2}}.\)
Giải
\(S_{ABC}=\frac{1}{2}AB.AC.sinA =\)\(\frac{1}{2}AB.AC.\sqrt{1-cos^{2}A}\)
\(=\frac{1}{2}AB.AC.\sqrt{1-\left ( \frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|} \right )^{2}}\)
\(=\frac{1}{2}\sqrt{\overrightarrow{AB}^{2}.\overrightarrow{AC}^{2}-(\overrightarrow{AB}.\overrightarrow{AC})^{2}}.\)
Bài 8 trang 98 sgk hình học 11
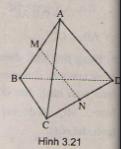
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat{BAC}=\widehat{BAD}=60^{0}.\) Chứng minh rằng:
a) \(AB ⊥ CD\);
b) Nếu \(M, N\) lần lượt là trung điểm của \(AB\) và \(CD\) thì \(MN ⊥ AB\) và \(MN ⊥ CD\).
Giải
(h.3.21)
a) \(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}(\overrightarrow{AD}-\overrightarrow{AC})\)
\(=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\)
\(=AB.AD.\cos\widehat{BAD}-AB.AC.\cos\widehat{BAC} =0\)
b) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN},\) (1)
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\) (2)
Cộng (1) với (2) theo vế với vế ta được: \(\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{BC})=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AC}-\overrightarrow{AB}).\)
Ta có \(\overrightarrow{AB}.\overrightarrow{MN}={1 \over 2}\overrightarrow {AB} .(\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} )\)
\(= {1 \over 2}(\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - A{B^2})\)
\(= {1 \over 2}(AB.AD.\cos\widehat{BAD}+AB.AC.\cos\widehat{BAC}-AB^2)\)
\(={1 \over 2}(AB.AD.\cos60^0+AB.AC.\cos60^0-AB^2)\)
\(={1 \over 2}\left({1 \over 2}AB^2+{1 \over 2}AB^2-AB^2\right)=0\) \(\Rightarrow AB ⊥ MN\).
Chứng minh tương tự ta được: \(CD ⊥ MN\).
congdong.edu.vn