Bài 6 trang 35 sách giáo khoa hình học lớp 11
Trong mặt phẳng tọa độ \(Oxy\), cho đường tròn tâm \(I(1;-3)\), bán kính \(2\). Viết phương trình ảnh của đường tròn \((I;2)\) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm \(O\) tỉ số \(3\) và phép đối xứng qua trục \(Ox\)
Lời giải:
Gọi \(I'\) là ảnh của \(I\) qua phép vị tự tâm \(O\) tỉ số \(3\).
Gọi \(I''\) là ảnh của \(I'\) qua phép đối xứng trục \(Ox\)
\(I' = {V_{(O,3)}} (I) = (3; -9)\), \(I'' = {D_{Ox}}(I') = ( 3;9)\). Đường tròn phải tìm có phương trình \((x-3)^{2}+(y-9)^{2}=36\)
Bài 7 trang 35 sách giáo khoa hình học lớp 11
Cho hai điểm \(A,B\) và đường tròn tâm \(O\) không có điểm chung với đường thẳng \(AB\). Qua mỗi điểm \(M\) chạy trên đường tròn \((O)\) dựng hình bình hành \(MABN\). Chứng mình rằng điểm \(N\) thuộc một đường tròn xác định
Lời giải:
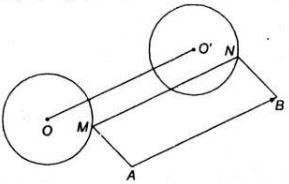
Vì \( \vec{MN}=\vec{AB}\) không đổi, nên có thể xem \(N\) là ảnh của \(M\) qua phép tịnh tiến theo \(\vec{AB}\). Do đó khi \(M\) chạy trên đường tròn \((O)\) thì \(N\) chạy trên đường tròn \((O')\) là ảnh của \((O)\) qua phép tịnh tiến theo \(\vec{AB}\).
Bài 4 trang 36 sách giáo khoa hình học lớp 11
Trong mặt phẳng tọa độ \(Oxy\), cho \(\vec{v} = (2;-1)\) và điểm \(M (-3;2)\). Ảnh của điểm \(M\) qua phép tịnh tiến theo vecto \(\vec{v}\) là điểm có tọa độ nào trong các tọa độ sau
(A) \((5;3)\)
(B) \((1;1)\)
(C) \(( -1;1)\)
(D) \(( 1; -1)\)
Giải
Giả sử \(M'(x,y)\) là ảnh của \(M\) qua phép tịnh tiến \(\vec v(2;-1)\) nên ta có:
\(\left\{ \matrix{
x = 2 + ( - 3) \hfill \cr
y = - 1 + 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr
y = 1 \hfill \cr} \right.\)
Vậy \(M'(-1;1)\)
Đáp án: C
Bài 5 trang 36 sách giáo khoa hình học lớp 11
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d\) có phương trình: \(3x - 2y + 1= 0\). Ảnh của đường thẳng \(d\) qua phép đối xứng trục \(Ox\) có phương trình là:
(A) \(3x + 2y + 1 =0\)
(B) \(-3x + 2y + 1 = 0\)
(C) \(3x + 2y - 1 = 0\)
(D) \(3x - 2y + 1 = 0\)
Giải
Biểu thức tọa độ của phép đối xứng trục \(Ox\) là
\(\left\{ \matrix{
x' = x \hfill \cr
y' = - y \hfill \cr} \right.\)
\(M(x;y)\in d\Leftrightarrow 3x-2y+1=0\)
\(\Leftrightarrow 3x'+2y'+1=0\Leftrightarrow M'(x';y')\in d'\)
Vậy \(d'\) có phương trình là: \(3x+2y+1=0\)
Đáp án : A
Bài 6 trang 36 sách giáo khoa hình học lớp 11
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(d\) có phương trình: \(3x - 2y - 1 = 0\). Ảnh của đường thẳng \(d\) qua phép đối xứng tâm \(O\) có phương trình là :
(A) \(3x + 2y + 1 = 0\)
(B) \(-3x + 2y - 1 = 0\)
(C) \(3x + 2y - 1 = 0\)
(D) \(3x - 2y -1 = 0\)
Giải
Biểu thức tọa độ của phép đối xứng tâm \(O\) là:
\(\left\{ \matrix{
x' = - x \hfill \cr
y' = - y \hfill \cr} \right.\)
\(M(x,y) \in d \Leftrightarrow 3x - 2y - 1 = 0 \)
\(\Leftrightarrow - 3x' + 2y' - 1 = 0 \Leftrightarrow M'(x';y') \in d'\)
Vậy phương trình \(d'\) là: \(-3x+2y-1=0\)
Đáp án: B
congdong.edu.vn