Bài 1 trang 33 sách giáo khoa hình học lớp 11
Cho tam giác \(ABC\). Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm \(B\) tỉ số \( \frac{1}{2}\) và phép đối xứng qua đường trung trực của \(BC\)
Lời giải
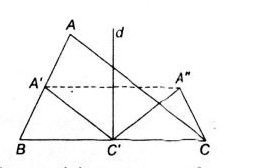
Gọi \(A',C'\) lần lượt là trung điểm của \(AB,BC\)
Phép vị tự tâm \(B\) tỉ số \( \frac{1}{2}\) biến tam giác \(ABC\) thành tam giác \(A'BC'\). Phép đối xứng qua đường trung trực của \(BC\) biến tam giác \(A'BC'\) thành tam giác \(A''CC'\). Vậy ảnh của tam giác ABC qua phép đồng dạng đã cho là tam giác \(A''CC'\).
Bài 2 trang 33 sách giáo khoa hình học lớp 11
Cho hình chữ nhật \(ABCD, AC\) và \(BD\) cắt nhau tại \(I\). Gọi \(H, K, L\) và \(J\) lần lượt là trung điểm của \(AD, BC, KC\) và \(IC\). Chứng minh hai hình thang \(JLKI\) và \(IHDC\) đồng dạng với nhau.
Lời giải:
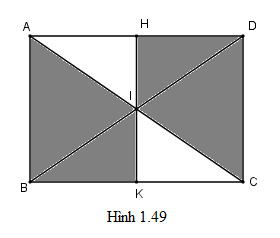
Phép vị tự tâm \(C\) tỉ số \(2\) biến hình thang \(JLKI\) thành hình thang \(IKBA\). Phép đối xứng tâm \(I\) biến hình thang \(IKBA\) thành hình thang \(IHDC\). Do đó hai hình thang \(JLKI\) và \(IHDC\) đồng dạng với nhau.
Bài 3 trang 33 sách giáo khoa hình học lớp 11
Trong mặt phẳng \(Oxy\) cho điểm \(I (1;1)\) và đường trong tâm \(I\) bán kính \(2\). Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm \(O\), góc \( 45^{\circ}\) và phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\).
Lời giải:
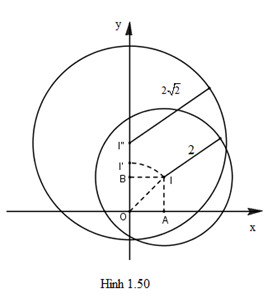
Phép quay tâm \(O\), góc \( 45^{\circ}\), biến \(I\) thành \(I'(0\);\( \sqrt{2}\)), phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\) biến \(I'\) thành \(I'' = (0; \)\( \sqrt{2}.\)\( \sqrt{2}\)) \(= (0;2)\). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm \(O\), góc \( 45^{\circ}\) và phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\) biến đường tròn \((I;2)\) thành đường tròn \((I'';2\)\( \sqrt{2}\)). Phương trình của đường tròn đó là
\(x^{2}\) + \((y-2)^{2} = 8\).
Bài 4 trang 33 sách giáo khoa hình học lớp 11
Cho tam giác \(ABC\) vuông tại \(A, AH\) là đường cao kẻ từ \(A\). Tìm một phép đồng dạng biến tam giác \(HBA\) thành tam giác \(ABC\)
Lời giải:
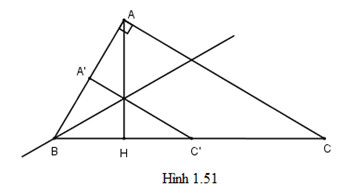
Gọi \(d\) là đường phân giác của \( \widehat{B}\). Ta có \({D_{d}}^{}\) biến \(∆HBA\) thành \(∆A'BC'\).
\({V_{(B,\frac{AC}{AH})}}^{}\) biến \(∆A'BC'\) thành \(∆ABC\).
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp \({D_{d}}^{}\) và \({V_{(B,\frac{AC}{AH})}}^{}\) sẽ
\( \bigtriangleup\)\(HBA\) thành \( \bigtriangleup\)\(ABC\)
congdong.edu.vn