Bài 1 trang 19 sách giáo khoa hình học lớp 11
Cho hình vuông \(ABCD\) tâm \(O\) (h.1.38)
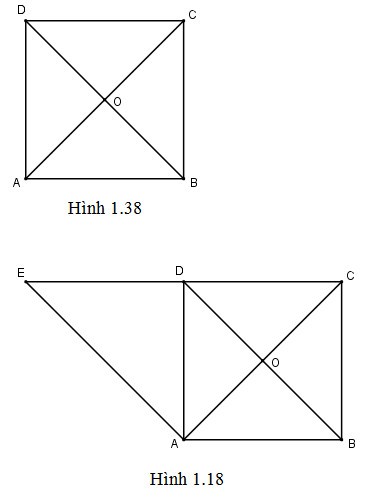
a, Tìm ảnh của điểm \(C\) qua phép quay tâm \(A\) góc \( 90^{\circ}\)
b, Tìm ảnh của đường thẳng \(BC\) qua phép quay tâm \(O\) góc \( 90^{\circ}\)
Lời giải: hình 1.18
a, Gọi \(E\) là điểm đối xứng với \(C\) qua tâm \(A\). Khi đó \({Q_{(A,90^{\circ})}}^{}\) (C) = \(E\)
b, \({Q_{(O,90^{\circ})}}(B) = C\), \({Q_{(O,90^{\circ})}} (C) = D\)
Vậy ảnh của đường thẳng \(BC\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) là đường thẳng \(CD\).
Bài 2 trang 19 sách giáo khoa hình học lớp 11
Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A(2;0)\) và đường thẳng \(d\) có phương trình \(x+y-2=0\). Tìm ảnh của \(A\) và \(d\) qua phép quay tâm \(O\) góc \( 90^{\circ}\)
Lời giải:
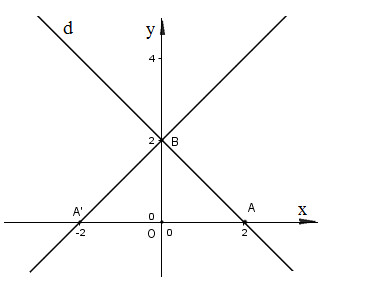
Lấy \(A(2;0), B(0;2)\) thuộc \(d\), Ta có ảnh của \(A\) và \(B\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) lần lượt là \(B=(0;2)\) và \(A' = (-2;0)\). Do đó ảnh của \(d\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) là đường thẳng \(BA'\) có phương trình \(x - y + 2 =0\).
congdong.edu.vn