Bài 1 trang 29 sách giáo khoa hình học lớp 11
Cho tam giác \(ABC\) có ba góc nhọn và \(H\) là trực tâm. Tìm ảnh của tam giác \(ABC\) qua phép vị tự tâm \(H\), tỉ số \( \frac{1}{2}\)
Lời giải:
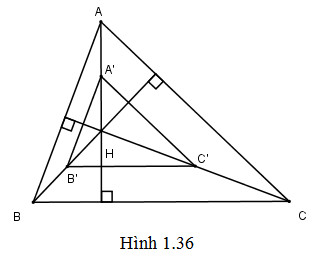
Ảnh của \(A, B, C\) lần lượt là trung điểm \(A', B', C'\) của các cạnh \(HA, HB, HC\)
Bài 2 trang 29 sách giáo khoa hình học lớp 11
Tìm tâm vị tự của hai đường tròn trong các trường hợp sau
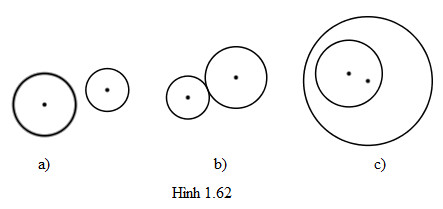
Lời giải:
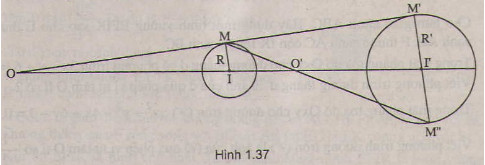
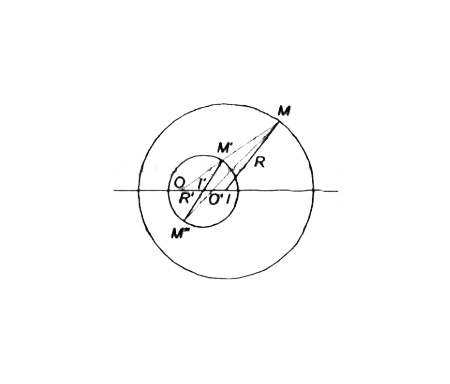
Lấy điểm \(M\) thuộc đường tròn \((I)\). Qua \(I'\) kẻ đường thẳng song song với \(IM\), đường thẳng này cắt đường tròn \((I')\) tại \(M'\) và \(M''\). Hai đường thẳng \(MM'\) và \(MM''\) cắt đường thẳng \(II'\) theo thứ tự \(O\) và \(O'\). Khi đó, \(O\) và \(O'\) là các tâm vị tự cần tìm
Vì hai đường tròn đã cho có bán kính khác nhau nên chúng có hai tâm vị tự là \(O\) và \(O'\), xác định trong từng trường hợp như sau ( xem hình vẽ):
a) Trường hợp 1( h1.37)
b) Trường hợp 2
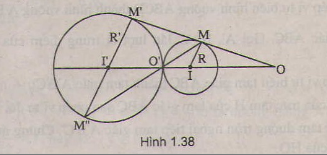
c) Trường hợp 3
Bài 3 trang 29 sách giáo khoa hình học lớp 11
Chứng minh rằng khi thực hiện liên tiếp hai phép vị tự tâm \(O\) sẽ được một phép vị tự tâm \(O\)
Lời giải:
Với mỗi điểm \(M\), gọi \(M'\) = \({V_{(O,k)}}(M)\), \(M''={V_{(O,p)}}(M')\). Khi đó: \(\overrightarrow{OM'}\) = \(k \overrightarrow{OM}\) , \(\overrightarrow{OM''}\) = \(p\overrightarrow{OM'}\) = \(pk\overrightarrow{OM}\). Từ đó suy ra \(M''= {V_{(O,pk)}} (M)\).
Vậy thực hiện liên tiếp hai phép vị tự \({V_{(O,k)}}^{}\) và \({V_{(O,p)}}^{}\) sẽ được phép vị tự \({V_{(O,pk)}}^{}\).
congdong.edu.vn