Lớp 11 - Toán học - Nâng cao Giải bài 21, 22, 23, 24, 25 trang 226, 227 SGK Đại số và Giải tích 11 Nâng cao
Câu 21 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Tìm đạo hàm của các hàm số sau :
a. \(y = {{a{x^3} + b{x^2} + c} \over {\left( {a + b} \right)x}}\) (a, b, c là các hằng số)
b. \(y = {\left( {{x^3} - {1 \over {{x^3}}} + 3} \right)^4}\)
c. \(y = {x^3}{\cos ^2}x\)
d. \(y = \sin \sqrt {4 + {x^2}} \)
e. \(y = \sqrt {1 + \tan \left( {x + {1 \over x}} \right)} \)
Giải:
a.
\(\eqalign{ & y' = \left[ {{a \over {a + b}}{x^2} + {b \over {a + b}}x + {c \over {\left( {a + b} \right)x}}} \right] \cr & = {{2a} \over {a + b}}x + {b \over {a + b}} - {c \over {\left( {a + b} \right){x^2}}} \cr & = {{2a{x^3} + b{x^2} - c} \over {\left( {a + b} \right){x^2}}} \cr} \)
b.
\(\eqalign{ & y' = 4{\left( {{x^3} - {1 \over {{x^3}}} + 3} \right)^3}\left( {3{x^2} + {3 \over {{x^4}}}} \right) \cr & = 12\left( {{x^3} - {1 \over {{x^3}}} + 3} \right)\left( {{x^2} + {1 \over {{x^4}}}} \right) \cr} \)
c. \(y' = 3{x^2}{\cos ^2}x - {x^3}\sin 2x = {x^2}\left( {3{{\cos }^2}x - x\sin 2x} \right)\)
d. \(y' = {x \over {\sqrt {4 + {x^2}} }}\cos \sqrt {4 + {x^2}} \)
e.
\(\eqalign{ & y' = {{1 - {1 \over {{x^2}}}} \over {2{{\cos }^2}\left( {x + {1 \over x}} \right)\sqrt {1 + \tan \left( {x + {1 \over x}} \right)} }} \cr & = {{{x^2} - 1} \over {2{x^2}{{\cos }^2}\left( {x + {1 \over x}} \right)\sqrt {1 + \tan \left( {x + {1 \over x}} \right)} }} \cr} \)
Câu 22 trang 227 SGK Đại số và Giải tích 11 Nâng cao
Cho hàm số \(y = m{x^3} + {x^2} + x - 5.\) Tìm m để :
a. y’ bằng bình phương của một nhị thức bậc nhất ;
b. y’ có hai nghiệm trái dấu ;
c. \(y’ > 0\) với mọi x.
Giải
a. Ta có: \(y' = 3m{x^2} + 2x + 1\)
Ta có \(y' = 3m{x^2} + 2x + 1\) là bình phương của một nhị thức bậc nhất khi và chỉ khi
\(\left\{ {\matrix{ {3m > 0} \cr {\Delta ' = 1 - 3m = 0} \cr } } \right.\Leftrightarrow m={1\over 3}\)
b. y’ có hai nghiệm trái dấu ⇔ \(3m.1 < 0 \Leftrightarrow m < 0\)
c.+) Với \(m = 0;\; y’ = 2x + 1 > 0 \Leftrightarrow x > - {1 \over 2}\) (không thỏa yêu cầu)
+) Với \(m ≠ 0\)
\(y' > 0,\forall x \in\mathbb R \Leftrightarrow \left\{ {\matrix{ {3m > 0} \cr {\Delta ' = 1 - 3m < 0} \cr } } \right. \Leftrightarrow m > {1 \over 3}\)
Câu 23 trang 227 SGK Đại số và Giải tích 11 Nâng cao
Giải các phương trình sau :
a. \(y' = 0\,voi\,y = {1 \over 2}\sin 2x + \sin x - 3\)
b. \(y' = 0,\,voi\,y = \sin 3x - 2\cos 3x - 3x + 4\)
Giải:
a. Ta có:
\(\eqalign{ & y' = \cos 2x + \cos x \cr & y' = 0 \Leftrightarrow \cos 2x + \cos x = 0 \cr & \Leftrightarrow 2{\cos ^2}x + \cos x - 1 = 0 \cr & \Leftrightarrow \left[ {\matrix{ {\cos x = - 1} \cr {\cos x = {1 \over 2}} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = \pi + k2\pi } \cr {x = \pm {\pi \over 3} + k2\pi } \cr } } \right.\,\,\left( {k \in Z} \right) \cr} \)
b.
\(\eqalign{ & y' = 3\cos 3x + 6\sin 3x - 3 \cr & y' = 0 \Leftrightarrow \cos 3x + 2\sin 3x = 1 \cr & \Leftrightarrow {1 \over {\sqrt 5 }}\cos 3x + {2 \over {\sqrt 5 }}\sin 3x = {1 \over {\sqrt 5 }} \cr & \Leftrightarrow \cos \left( {3x - \alpha } \right) = \cos \alpha \,\left( {voi\,\cos \alpha = {1 \over {\sqrt 5 }}} \right) \cr & \Leftrightarrow \left[ {\matrix{ {3x - \alpha = \alpha + k2\pi } \cr {3x - \alpha = - \alpha + k2\pi } \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = {{2\alpha } \over 3} + k{{2\pi } \over 3}} \cr {x = k{{2\pi } \over 3}} \cr } } \right. \cr} \)
Câu 24 trang 227 SGK Đại số và Giải tích 11 Nâng cao
Cho hyperbol (H) xác định bởi phương trình \(y = {1 \over x}\)
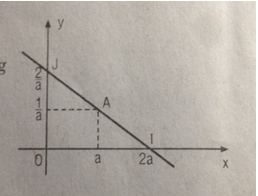
a. Tìm phương trình tiếp tuyến (T) của (H) tại tiếp điểm A có hoành độ a (với a ≠ 0)
b. Giả sử (T) cắt trục Ox tại điểm I và cắt trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn thẳng IJ. Từ đó suy ra cách vẽ tiếp tuyến (T).
c. Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A.
Giải:
Với mọi x ≠ 0, ta có : \(f'\left( x \right) = - {1 \over {{x^2}}}\)
a. Phương trình tiếp tuyến (T) tại điểm \(A\left( {a;{1 \over a}} \right)\) là :
\(y = - {1 \over {{a^2}}}\left( {x - a} \right)\,\,hay\,y = - {1 \over {{a^2}}}x + {2 \over a}\)
b. Ta nhận thấy \(I\left( {2a;0} \right);\,J\left( {0;{2 \over a}} \right)\)
Kiểm tra dễ dàng rằng điểm \(A\left( {a;{1 \over a}} \right)\) là trung điểm của đoạn IJ. Từ đó suy ra cách vẽ tiếp tuyến (T). Đó là đường thẳng IJ.
c. Diện tích tam giác OIJ là :
\(S = {1 \over 2}\left| {OI} \right|.\left| {OJ} \right| = {1 \over 2}\left| {2a.{2 \over a}} \right| = 2\) (đvdt)
Vì S không phụ thuộc vào a nên diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A ϵ (H)
Câu 25 trang 227 SGK Đại số và Giải tích 11 Nâng cao
Một điểm M chuyển động trên parabol \(y = - {x^2} + 17x - 66\) theo hướng tăng của x. Một người quan sát đứng ở vị trí P(2 ; 0)
Hãy xác định các giá trị của hoành độ điểm M để người quan sát có thể nhìn thấy được điểm M.
Giải:
Người quan sát thấy được điểm M nếu M thuộc phần parabol nằm trong góc tạo bởi hai tiếp tuyến của parabol đi qua P(2 ; 0). Điều đó tương đương với bất đẳng thức kép x1 ≤ m ≤ x2; trong đó m là hoành độ của điểm M, x1 và x2 là hoành độ hai tiếp điểm. Ta cần xác định x1 và x2.
Phương trình đường thẳng (d) đi qua P(2 ; 0) với hệ số góc bằng k là :
\(y = k(x – 2)\)
Để (d) là tiếp tuyến của parabol \(y = - {x^2} + 17x - 66\) thì ta phải có :
\(\left\{ {\matrix{ { - {x^2} + 17x - 66 = k\left( {x - 2} \right)} \cr { - 2x + 17 = k} \cr } } \right.\)
Khử k, ta được :
\({x^2} - 4x - 32 = 0 \Leftrightarrow \left[ {\matrix{ {{x_1}= - 4} \cr {{x_2} = 8} \cr } } \right.\)
(x1 và x2 chính là hai hoành độ tiếp điểm của hai tiếp tuyến kẻ từ P(2 ; 0) đến parabol đã cho).
Vậy người quan sát có thể nhìn được các điểm M thuộc parabol đã cho, nếu hoành độ điểm M thuộc đoạn [-4 ; 8].
congdong.edu.vn