Lớp 11 - Toán học - Nâng cao Giải bài 1, 2, 3, 4, 5, 6 trang 91 SGK Hình học 11 Nâng cao
Câu 1 trang 91 SGK Hình học 11 Nâng cao
Ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có đồng phẳng không nếu một trong hai điều sau đây xảy ra ?
a. Có một vecto trong ba vecto đó bằng \(\overrightarrow 0 \)
b. Có hai vecto trong ba vecto đó cùng phương.
Giải
a. Giả sử \(\overrightarrow a = \overrightarrow 0 .\) Áp dụng định lí 1 : \(\overrightarrow a = 0.\overrightarrow b + 0.\overrightarrow c \) nên \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
b. Giả sử \(\overrightarrow a ,\overrightarrow b \) cùng phương, khi đó có số k sao cho \(\overrightarrow a = k\overrightarrow b \)
\( \Rightarrow \overrightarrow a = k\overrightarrow b + 0.\overrightarrow c \) do đó \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
Câu 2 trang 91 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD.
a. Chứng minh rằng nếu ABCD là hình bình hành thì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \). Điều ngược lại có đúng không ?
b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \)
Giải
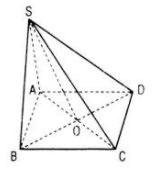
a. Ta có:
\(\eqalign{ & \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \cr & \Leftrightarrow \overrightarrow {SB} - \overrightarrow {SC} = \overrightarrow {SA} - \overrightarrow {SD} \Leftrightarrow \overrightarrow {CB} = \overrightarrow {DA} \cr} \)
⇔ ABCD là hình bình hành.
b. Ta có:
\(\eqalign{ & \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} + \overrightarrow {SO} + \overrightarrow {OC} + \overrightarrow {SO} + \overrightarrow {OD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \,\,\left( * \right) \cr} \)
Nếu ABCD là hình bình hành thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) suy ra
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) (do (*))
Ngược lại, giả sử \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} ,\) ta có (*).
Gọi M, N lần lượt là trung điểm của AC, BD thì :
\(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {OM} ,\overrightarrow {OB} + \overrightarrow {OD} = 2\overrightarrow {ON} \)
Từ (*) suy ra \(2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 ,\) điều này chứng tỏ O, M, N thẳng hàng
Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành.
Câu 3 trang 91 SGK Hình học 11 Nâng cao
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
Giải
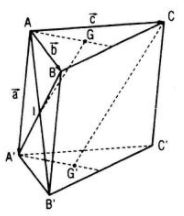
Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Thì \(\overrightarrow {AG} = {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right),\overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)\)
Do đó, \(\overrightarrow {GI} = \overrightarrow {AI} - \overrightarrow {AG} = {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 6}\)
Mặt khác : \(\overrightarrow {AG'} = {1 \over 3}\left( {\overrightarrow {AA'} + \overrightarrow {AB'} + \overrightarrow {AC'} } \right) = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right)\)
\( \Rightarrow \overrightarrow {CG'} = \overrightarrow {AG'} - \overrightarrow {AC} = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right) - \overrightarrow c \)
\(= {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 3}\)
Vậy \(\overrightarrow {CG'} = 2\overrightarrow {GI} .\) Ngoài ra, điểm G không thuộc đường thẳng CG’ nên GI và CG’ là hai đường thẳng song song.
Câu 4 trang 91 SGK Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Giải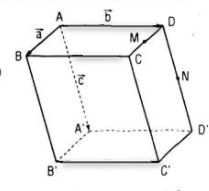
Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow c .\)
Vì G’ là trọng tâm tứ diện BCC’D’ nên \(\overrightarrow {AG'} = {1 \over 4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AC'} + \overrightarrow {AD'} } \right)\)
Và G là trọng tâm tứ diện A’D’MN nên
\(\eqalign{ & \overrightarrow {AG} = {1 \over 4}\left( {\overrightarrow {AA'} + \overrightarrow {AD'} + \overrightarrow {AM} + \overrightarrow {AN} } \right) \cr & \Rightarrow \overrightarrow {GG'} = \overrightarrow {AG'} - \overrightarrow {AG} \cr& = {1 \over 4}\left( {\overrightarrow {A'B} + \overrightarrow {D'C} + \overrightarrow {MC'} + \overrightarrow {ND'} } \right) \cr & = {1 \over 4}\left( {\overrightarrow a - \overrightarrow c + \overrightarrow a - \overrightarrow c + {1 \over 2}\overrightarrow a + \overrightarrow c + {1 \over 2}\overrightarrow c } \right) \cr & = {1 \over 8}\left( {5\overrightarrow a - \overrightarrow c } \right) = {1 \over 8}\left( {5\overrightarrow {AB} - \overrightarrow {AA'} } \right) \cr} \)
Do đó \(\overrightarrow {AB} ,\overrightarrow {AA'} ,\overrightarrow {GG'} \) đồng phẳng. Mặt khác, G không thuộc mặt phẳng (ABB’A’) nên đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Câu 5 trang 91 SGK Hình học 11 Nâng cao
Trong không gian cho tam giác ABC.
a. Chứng minh rằng nếu điểm M thuộc mp(ABC) thì có ba số x, y, z mà x + y + z = 1 sao cho \(\overrightarrow {OM} = \overrightarrow {xOA} + \overrightarrow {yOB} + \overrightarrow {zOC} \) với mọi điểm O.
b. Ngược lại, nếu có một điểm O trong không gian saao cho \(\overrightarrow {OM} = \overrightarrow {xOA} + \overrightarrow {yOB} + \overrightarrow {zOC} ,\) trong đó x + y + z = 1 thì điểm M thuộc mp(ABC).
Giải
a. Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là hai vecto không cùng phương nên điểm M thuộc mp(ABC) khi và chỉ khi có \(\overrightarrow {AM} = l\overrightarrow {AB} + m\overrightarrow {AC} \)
hay \(\overrightarrow {OM} - \overrightarrow {OA} = l\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) + m\left( {\overrightarrow {OC} - \overrightarrow {OA} } \right)\) với mọi điểm O
tức là \(\overrightarrow {OM} = \left( {1 - l - m} \right)\overrightarrow {OA} + l\overrightarrow {OB} + m\overrightarrow {OC} \)
đặt \(1 - l - m = x,l = y,m = z\) thì \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \) với \(x + y + z = 1.\)
b. Giả sử \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \) với \(x + y + z = 1,\) ta có :
\(\eqalign{ & \overrightarrow {OM} = \left( {1 - y - z} \right)\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \cr & hay\,\overrightarrow {OM} - \overrightarrow {OA} = y\overrightarrow {AB} + z\overrightarrow {AC} \cr & \text{ tức là }\overrightarrow {AM} = y\overrightarrow {AB} + z\overrightarrow {AC} \cr} \)
Mà \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương nên M thuộc mặt phẳng (ABC)
Câu 6 trang 91 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.
Giải
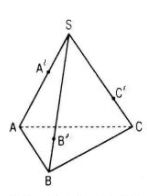
Ta có: \(\overrightarrow {SA} = a\overrightarrow {SA'} ,\;\overrightarrow {SB} = b\overrightarrow {SB'} ,\;\overrightarrow {SC} = c\overrightarrow {SC} .\)
Gọi G là trọng tâm của tam giác ABC thì
\(\eqalign{ & \overrightarrow {SG} = {1 \over 3}.\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) \cr & Vay\,\overrightarrow {SG} = {a \over 3}\overrightarrow {SA'} + {b \over 3}\overrightarrow {SB'} + {c \over 3}\overrightarrow {SC'} \cr} \)
Mặt phẳng (A’B’C’) đi qua G khi và chỉ khi 4 điểm G, A’, B’, C’ đồng phẳng, nên theo kết quả bài tập 5 (SGK trang 91) , điều đó xảy ra nếu và chỉ nếu \({a \over 3} + {b \over 3} + {c \over 3} = 1\) , tức là: a + b + c = 3.
congdong.edu.vn