Lớp 11 - Toán học - Nâng cao Giải bài 20, 21, 22, 23, 24 trang 23 SGK Hình học 11 Nâng cao

Câu 20 trang 23 SGK Hình học 11 Nâng cao

Chứng tỏ rẳng hai hình chữ nhật cùng kích thước (cùng chiều dài và chiều rộng) thì bằng nhau

Giải

Giả sử hai hình chữ nhật ABCD và A’B’C’D’ có \(AB = CD = A’B’= C’D’, AD = BC = A’D = B’C’\).

Khi đó ABC và A’B’C’ là hai tam giác vuông bằng nhau, do đó có phép dời hình F biến tam giác ABC thành tam giác A’B’C’

Khi đó phép dời hình F biến trung điểm O của AC thành trung điểm O’ của A’C’

Nhưng vì O và O’ lần lượt cũng là trung điểm của BD và B’D’ nên F cũng biến D thành D’

Vậy F biến ABCD thành A’B’C’D’, nên theo định nghĩa, hai hình chữ nhật đó bằng nhau

Câu 21 trang 23 SGK Hình học 11 Nâng cao

a. Chứng minh rằng hai tứ giác lồi có cặp cạnh tương ứng bằng nhau và một cặp đường chéo tương ứng bằng nhau thì bằng nhau

b. Chứng minh rằng hai tứ giác lồi có các cặp cạnh tương ứng bằng nhau và một cặp góc tương ứng bằng nhau thì bằng nhau

c. Hai tứ giác lồi có các cặp cạnh tương ứng bằng nhau thì có bằng nhau hay không?

Giải

a.

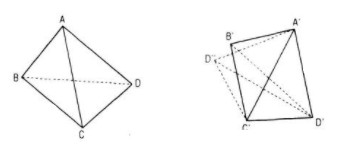
Giả sử hai tứ giác lồi ABCD và A’B’C’D’ có \(AB = A’B’; BC = B’C’; CD = C’D’, DA = D’A’\) và \(AC = A’C’\)

Khi đó hai tam giác ABC và A’B’C’ bằng nhau nên có phép dời hình F biến ba điểm A, B, C lần lượt thành ba điểm A’, B’, C’

Gọi D” là điểm đối xứng với điểm D’ qua đường thẳng A’C’ thì hai tam giác A’C’D’ và A’C’D” bằng nhau và theo giả thiết, cùng bằng tam giác ACD

Bởi vậy phép F chỉ có thể biến điểm D thành điểm D’ hoặc D” (do phép dời hình bảo toàn độ dài đoạn thẳng)

Vì ABCD là tứ giác lồi nên hai đoạn thẳng AC và BD cắt nhau, A’B’C’D’ cũng là tứ giác lồi nên hai đoạn thẳng nên hai đoạn thẳng A’C’ và B’D’ cắt nhau, và do đó hai đoạn thẳng A’C’ và B’D” không cắt nhau

Từ đó ta suy ra F biến D thành D’

Vậy F biến tứ giác ABCD thành tứ giác A’B’C’D’ và do đó hai tứ giác đó bằng nhau

b. Giả sử hai tứ giác ABCD và A’B’C’D’ có \(AB = A’B’, BC = B’C’, CD = C’D’, DA = D’A’\) và góc ABC bằng góc A’B’C’

Khi đó \(AC = A’C’\) và ta đưa về trường hợp ở câu a)

c. Có thể không bằng nhau

Hai hình thoi có cạnh bằng nhau nhưng có thể là hai hình không bằng nhau (vì phép dời hình biến góc thành góc bằng nó)

Câu 22 trang 23 SGK Hình học 11 Nâng cao

Đa giác lồi n cạnh gọi là n – giác đều nếu tất cả các cạnh của nó bằng nhau và tất cả các góc của nó bằng nhau khi và chỉ khi chúng có cạnh bằng nhau

Giải

Theo định nghĩa, hai n-giác đều bằng nhau thì cạnh bằng nhau.

Ngược lại, giả sử hai n-giác đều A₁A₂…A_n có cạnh bằng nhau

Khi đó nếu gọi O và O’ lần lượt là tâm các đường tròn ngoại tiếp hai đa giác đó thì hai tam giác OA₁A₂ và O’A’₁A’₂ bằng nhau

Vậy có phép dời hình F biến tam giác OA₁A₂ thành tam giác O’A’₁A’₂.

Vì hai tam giác OA₂A₃ và O’A’₂A’₃ cũng bằng nhau nên F biến điểm A₃ thành điểm A’₃ (vì A₃ không thể biến thành A’₁)

Lập luận tương tự ta cũng có F biến các điểm A₄,…, A_n lần lượt thành các điểm A₄ ,…, A_n

Như vậy hai đa giác đều đã cho bằng nhau

Câu 24 trang 23 SGK Hình học 11 Nâng cao

Câu 23 trang 23 SGK Hình học 11 Nâng cao

Hình H₁ gồm ba đường tròn \(\left( {{O_1};{r_1}} \right),\left( {{O_2};{r_2}} \right)\) và \(\left( {{O_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Hình H₂ gồm ba đường tròn \(\left( {{I_1};{r_1}} \right),\left( {{I_2};{r_2}} \right)\) và \(\left( {{I_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H₁ và H₂ bằng nhau = r

Giải

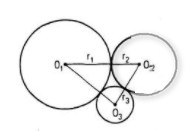
Ta có

\({{O_1}{O_2} = {r_1} + {\rm{ }}{r_2} = {I_1}{I_2}}\)
\({{O_2}{O_3} = {r_2} + {\rm{ }}{r_3} = {I_2}{I_3}} \)
\({{O_3}{O_1} = {r_3} + {\rm{ }}{r_1} = {I_3}{I_1}} \)

Suy ra \(\Delta {O_1}{O_2}{O_3} = \Delta {I_1}{I_2}{I_3}\) nên có phép dời hình F biến ba điểm O₁, O₂, O₃ lần lượt thành ba điểm I₁, I₂, I₃

Hiển nhiên khi đó F biến ba đường tròn \(({O_{1}}{\rm{; }}{r_1}),{\rm{ }}({O_2};{\rm{ }}{r_2}),{\rm{ }}({O_3};{\rm{ }}{r_3})\) lần lượt thành ba đường tròn \(({I_1};{r_1}),({I_2};{r_2}),({I_3};{r_3})\), tức là biến hình H₁ thành hình H₂

Vậy hai hình H₁ và H₂ bằng nhau

Câu 24 trang 23 SGK Hình học 11 Nâng cao

Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau

Giải

Một đường thẳng đi qua tâm O của hình bình hành thì chia hình bình hành đó thành hai phần bằng nhau, vì phép đối xứng qua tâm O sẽ biến phần này thành phần kia

Bởi vậy, nếu cho hai hình bình hành, ta chỉ cần vẽ đường thẳng đi qua tâm của chúng thì đường thẳng đó sẽ chia mỗi hình bình hành thành hai phần bằng nhau

Nếu tâm hai hình bình hành trùng nhau thì mọi đường thẳng đi qua tâm đó đều chia mỗi hình bình hành thành hia phần bằng nhau

                                                                                                    congdong.edu.vn