Lớp 11 - SBT Vật lí Giải bài 27.8, 27.9, 27.10 trang 71, 72 Sách bài tập Vật Lí 11

Bài 27.8 trang 71 Sách bài tập (SBT) Vật Lí 11

Một khối bán trụ có chiết suất n = 1,41 \( \approx \sqrt 2 \). Trong một mặt phẳng của tiết diện vuông góc, có hai tia song song tới gặp mặt phẳng của bán trụ với góc tới i = 45° ở A và O (Hình 27.4)

a) Tính góc lệch ứng với tia tới so sau khi ánh sáng khúc xạ ra không khí.

b) Xác định đường truyền của tia tới SA.

Trả lời:

a) Tia SO có tia khúc xạ OJ truyền theo phương một bán kính (HÌnh 27.1G). Do đó tại J, góc tới bằng 0. Tia sáng truyền thẳng qua không khí.

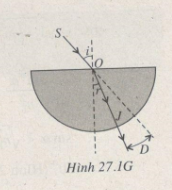
Ta có D = i – r = 45⁰ – 30⁰ = 15⁰

b) Đối với tia tới SA, môi trường bán trụ có thể coi như có hai pháp tuyến vuông góc nhau.

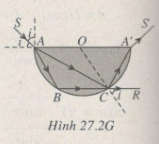
Trong hai trường hợp ta luôn có: i = 45⁰, r = 30⁰

Do đó kết hợp các tính chất hình học, ta có hai đường đi của tia sáng như sau (Hình 27.2G):

+ SABCA’S’

+ SACR

(A, B, C, A’ chia nửa đường tròn thành ba phần bằng nhau).

Bài 27.9 trang 72 Sách bài tập (SBT) Vật Lí 11

Một khối thuỷ tinh có tiết diện thẳng như Hình 27.5, đặt trong không khí (ABCD là hình vuông ; CDE là tam giác vuông cân). Trong mặt phẳng của tiết diện thẳng, chiếu một chùm tia sáng đơn sắc hẹp SI vuông góc với DE (IE < ID).

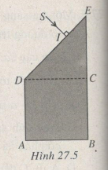
Chiết suất của thuỷ tinh là n = 1,5. Vẽ đường đi của tia sáng trong khối thuỷ tinh. Phương của tia ló hợp với pháp tuyến của mặt mà tia sáng ló ra một góc bằng bao nhiêu ?

Trả lời:

Tia SI truyền thẳng tới mặt EC tại J.

sini_gh = 1/n = 2/3 à i_gh ≈ 42⁰

i_J > i_gh: phản xạ toàn phần

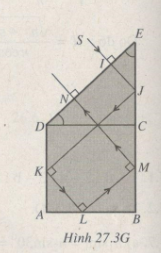
Tia phản xạ từ J tới sẽ phản xạ toàn phần lần lượt tại DA, AB, BC, và ló ra khỏi DE ở N theo phương vuông góc (tức là song song với SI nhưng ngược chiều (Hình 27.3G). Góc phải tìm là 0⁰.

Bài 27.10 trang 72 Sách bài tập (SBT) Vật Lí 11

Một sợi quang hình trụ với lõi có chiết suất n1 = 1,5 và phần bọc ngoài có chiết suất n₂ = 1,41. Chùm tia tới hội tụ tại mặt trước của sợi quang với góc 2α (Hình 27.6).

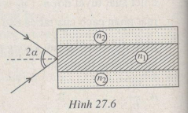
Xác định góc α để tất cả tia sáng trong chùm đều truyền đi được trong sợi quang.

Trả lời:

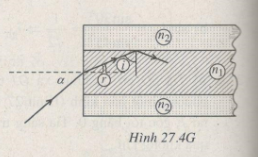
Ta phải có: i > i_gh

sini > n₂/n₁ --> cosr > n₂/n₁

Nhưng:

\({\mathop{\rm cosr}\nolimits} = \sqrt {1 - {{\sin }^2}r} = \sqrt {1 - {{{{\sin }^2}\alpha } \over {n_1^2}}} \)

Do đó:

\(\eqalign{
& 1 - {{{{\sin }^2}\alpha } \over {n_1^2}} > {{n_2^2} \over {n_1^2}} \cr
& \sin \alpha < \sqrt {n_1^2 - n_2^2} \approx 0,5 = \sin {30^0} \cr
& \Rightarrow 2\alpha < {60^0} \cr} \)

congdong.edu.vn