Lớp 11 - Vật lí - Nâng cao Giải bài C1, 1, 2, 3, 4 trang 260, 263 SGK Vật lí 11 Nâng cao
Câu C1 trang 260 SGK Vật lí 11 Nâng cao
Nếu sử dụng thị kính như một kính lúp để quan sát ảnh A1B1, thì A1B1 phải được đặt ở đâu?
Giải
Nếu sử dụng thị kính như một kính lúp để quan sát ảnh A1B1 thì A1B1 phải được đặt trong khoảng tiêu cự của thị kính.
Bài 1 trang 263 SGK Vật lí 11 Nâng cao
Điều chỉnh kính hiển vi khi ngắm chừng phải
A. thay đổi khoảng cách giữa vật và vật kính bằng cách đưa, toàn bộ ống kính lên hay xuống sao cho nhìn thấy ảnh của vật to và rõ nhất.
B. thay đổi khoảng cách giữa vật và vật kính bằng cách giữ nguyên toàn bộ ống kính, đưa vật lại gần vật kính sao cho nhìn thấy ảnh của vật to và rõ nhất.
C. thay đổi khoảng cách giữa vật kính và thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất.
D. thay đổi khoảng cách giữa vật và thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất.
Giải
A là câu đúng.
Bài 2 trang 263 SGK Vật lí 11 Nâng cao
Chọn câu đúng.
Công thức về số bội giác của kính hiển vi trong trường hợp ngắm chừng ở vô cực là:
A.\({G_\infty } = {{2\delta .Đ } \over {{f_1}{f_2}}}\) B.\({G_\infty } = {{\delta .Đ } \over {2{f_1}{f_2}}}\)
C.\({G_\infty } = {{{f_1}{f_2}} \over {\delta Đ }}\) D.\({G_\infty } = {{\delta .Đ } \over {{f_1}{f_2}}}\)
Giải
D là đáp án đúng.
Bài 3 trang 263 SGK Vật lí 11 Nâng cao
Một kính hiển vi có vật kính với tiêu cự f1 = 1 cm và tai kính với tiêu cự f2 = 4 cm. Hai thấu kính cách nhau 17 cm. Tính độ bội giác khi ngắm chừng ở vô cực. Lấy Đ = 25 cm
Giải
f1 = 1cm, f2 = 4cm, O1O2 = 17 cm
\( \Rightarrow \delta = {O_1}{O_2} - \left( {{f_1} + {f_2}} \right) = 17 - 5 = 12\left( {cm} \right)\)
\( \Rightarrow {G_\infty } = {{\delta Đ } \over {{f_1}{f_2}}} = {{12.25} \over {1.4}} = 75\)
Bài 4 trang 263 SGK Vật lí 11 Nâng cao
Một kính hiển vi có vật kính với tiêu cự f1 = 4mm, thị kính với tiêu cự f2= 20mm và độ dài quang học \(\delta \)= 156 mm. Người quan sát có mắt bình thường với điểm cực cận cách mắt 1 khoảng Đ = 250mm, Mắt đặt tại tiêu điểm ảnh của thị kính. Hãy xác định:
a) Khoảng cách từ vật đến vật kính trong trường hợp ngắm chừng này.
b) Số bội giác trong trường hợp ngắm chừng ở vô cực.
c) Góc trông ảnh, biết \(AB = 2\mu m\)
Giải
f1 = 4mm = 0,4 cm, f2 = 20mm = 2cm, \(\delta \) = 15,6 cm,
O1O2 = f1 + \(\delta \) + f2 = 18cm
a) Mắt bình thường có Đ = 25 cm. đặt tại tiêu điểm ảnh của thị kính => \(l = 2cm\).
Ta có sơ đồ tạo ảnh
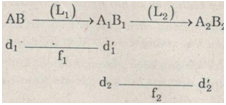
* Ngắm chừng ở cực cận:
\({d'_2} = -(Đ - l) = -(25 - 2) = -23 cm\).
\( \Rightarrow {d_2} = {{{d_2}'{f_2}} \over {{d_2}' - {f_2}}} = {{ - 23.2} \over { - 23 - 2}} = 1,84cm\)
\( \Rightarrow d{'_1} = {O_1}{O_2} - {d_2} = \left( {{f_1} + {f_2} + \delta } \right) - {d_2}\)
\( = \left( {0,4 + 2 + 15,6} \right) - 1,84 = 16,16cm\)
\( \Rightarrow {d_1} = {{{d_1}'{f_1}} \over {{d_1}' - {f_1}}} = {{16,16.0,4} \over {16,16 - 0,4}} = 0,41015cm\)
Vậy khoảng cách từ vật đến vật kính là 0,41015 cm.
* Ngắm chừng ở cực viễn (vô cực):
\({d_2}' = -\left( {O{C_V} - l} \right) = - \infty \Rightarrow {d_2} = {f_2} = 2cm\)
\({d_1}' = {O_1}{O_2} - {d_2} = 18 - 2 = 16cm\)
\({d_1} = {{{d_1}'.{f_1}} \over {{d_1}' - {f_1}}} = 0,41026\)
Vậy khoảng cách từ vật dên vật kính trong trường hợp này là:
\(0,41015cm{\rm{ }} \le {\rm{ }}d{\rm{ }} \le {\rm{ }}0,41026cm.\)
b) \({G_\infty } = {{\delta Đ} \over {{f_1}{f_2}}} = {{15,6.25} \over {0,4.2}} = 487,5\)
c) Cho \(AB = 2\mu m = {2.10^{ - 6}}\left( m \right)\)
Ta có \({G_\infty } = {{\tan \alpha } \over {\tan {\alpha _0}}} = {\alpha \over {{\alpha _0}}} \Rightarrow \alpha = {G_\infty }.{\alpha _0}\)
Với \({\alpha _0} = {{AB} \over Đ } = {{{{2.10}^{ - 6}}} \over {25}} = {8.10^{ - 6}}\left( {rad} \right)\)
Vậy \(\alpha = {G_\infty }.{\alpha _0} = 487,5 \times {8.10^{ - 6}} = 3,{9.10^{ - 3}}\left( {rad} \right)\)
congdong.edu.vn